Algorithms: Sorting

High level review of classic sorting algorithms with Haskell.

What do we mean by Sorted?

For a sorted list, every element is smaller or equals to the next one. From this very definition we can check if a list is sorted by

1. Checking that the first element is less than or equal to the next one
2. Recursively check that the rest is sorted

isSorted [] = True
isSorted [x] = True
isSorted (x0:x1:xs) = (x0 <= x1) && isSorted(x1:xs)

Recursive Sorting algorithms

These sorting algorithms divide the given list into 2 subproblems of roughly the same size. There are two prominent algorithms in this category.

• Merge sort - uses a linear time algorithm to combine the two sorted lists
• Quick sort - uses a linear time algorithm to partition values into left (less than) and right (more than) a pivot.

Merge Sort

Given 2 already sorted lists, compare only the first element from both lists. The smaller value got appended to the result. Repeat this process with that smaller value removed from consideration.

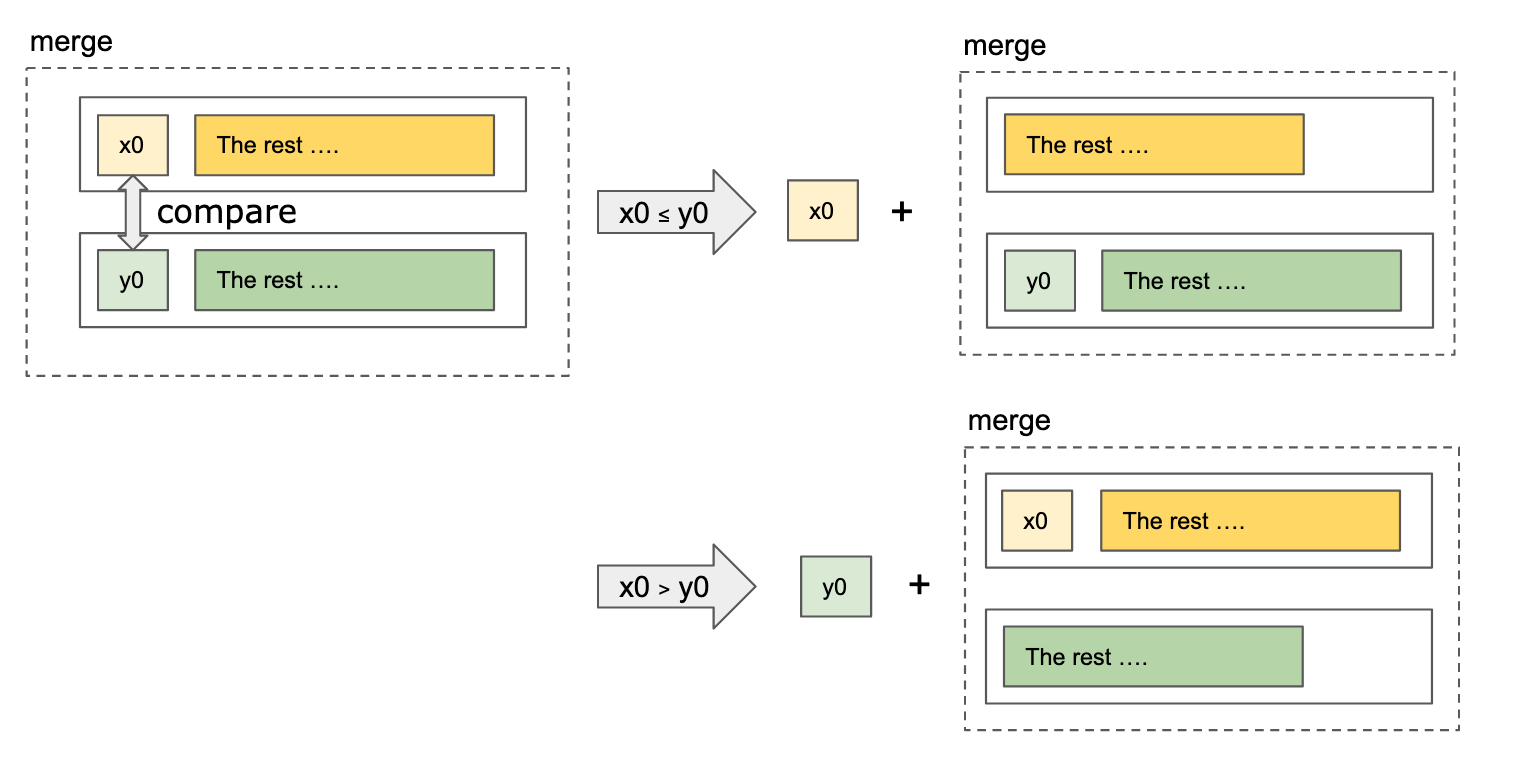
merge :: Ord a => [a] -> [a] -> [a]
merge [] [] = []
merge xs [] = xs
merge [] ys = ys
merge (x:xs) (y:ys) 
  | x <= y    = x : merge xs (y:ys)
  | otherwise = y : merge (x:xs) ys

The full merge sort algorithm simply halves a given unsorted list, recursive call to sort each half. Afterward, combining the two sorted halves with the merge algorithm defined above.

split :: [a] -> ([a], [a])
split [] = ([], [])
split xs = splitAt (length(xs) `div` 2) xs

mSort :: Ord a => [a] -> [a]
mSort [] = []
mSort [x] = [x]
mSort xs = merge (mSort left) (mSort right)
  where 
    (left, right) = split xs

Quicksort

Here is a classic intro in showing the expressive power of Haskell.

1. Uses the first value x as a pivot point. Loop and separate values into ≤ x group and >x group.
2. Recursively calls quick sort into the two groups
3. join the ≤ x, x, and >x group together

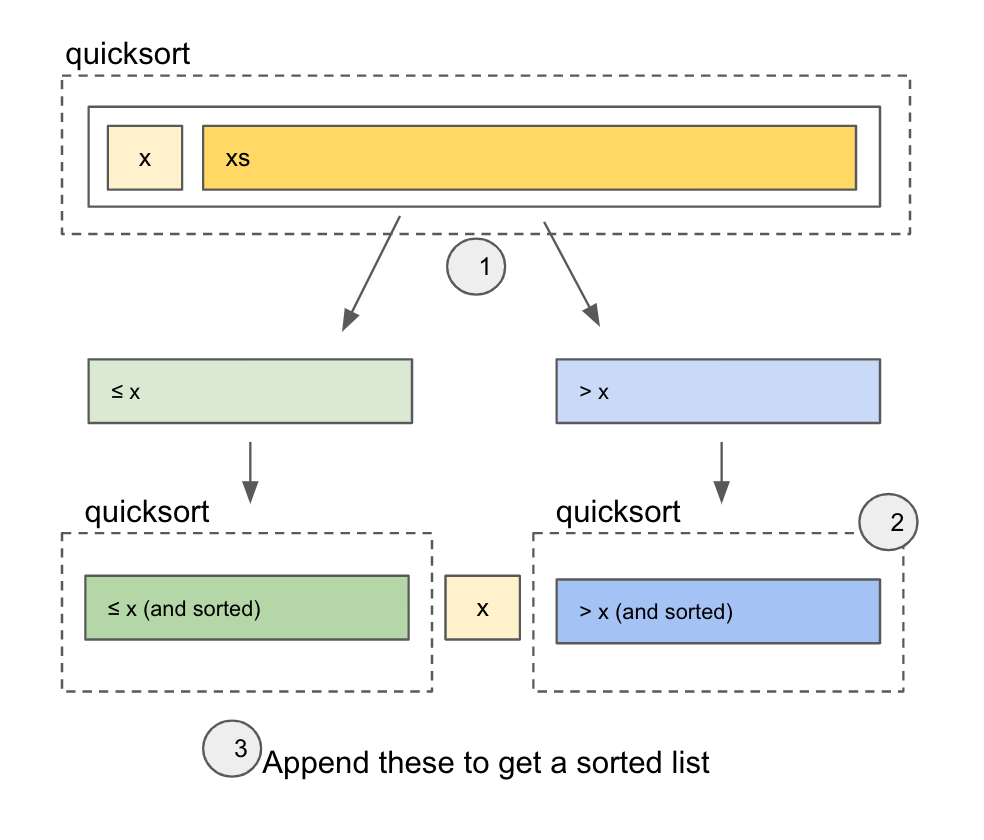
There's no guarantee that the two groups are partitioned into equal sizes. There exists a way to do quick sort in-place without additional memory, however.

qSort :: Ord a => [a] -> [a]
qSort [] = []
qSort (x:xs) = qSort(left) ++ [x] ++ qSort(right)
  where
      left  = [y | y <- xs, y <= x]
      right = [y | y <- xs, y >  x]

Quadratic time sorting algorithms

Also known as O(n^2). These algorithms have a similar outline where the problem size is reduced by 1 per iteration of execution. Each iteration itself takes a linear time, making this O (n^2) in total.

Selection Sort

Finds a min value from a list, adds to answer, repeats on the remaining list excluding the selected min value.

sSort :: Ord a => [a] -> [a]
sSort [] = []
sSort xs = min : sSort(remaining)
  where min = minimum xs
        remaining = delete min xs

Insertion Sort

Maintain a sorted list (the answer), starting from empty. Insert a new value one element at a time from original lists at the right index in the sorted answer.

orderedInsert :: Ord a => a -> [a] -> [a]
orderedInsert a [] = [a]
orderedInsert a (x:xs)
  | a < x     = a:x:xs
  | otherwise = x:(orderedInsert a xs)

iSort :: Ord a => [a] -> [a]
iSort [] = []
iSort (x:xs) = orderedInsert x (iSort xs)

Bubble Sort

Closely related to selection sort. Instead of selecting a max value, bubbles the value as we compare each element.

bSort :: Ord a => [a] -> [a]
bSort [] = []
bSort xs = bSort(init bubbled) ++ [last bubbled]
  where
    bubbled = bubble xs

bubble :: Ord a => [a] -> [a]
bubble [] = []
bubble [x] = [x]
bubble (x0:x1:xs)
  | x0 < x1   = x0 : bubble( x1:xs )
  | otherwise = x1 : bubble( x0:xs )